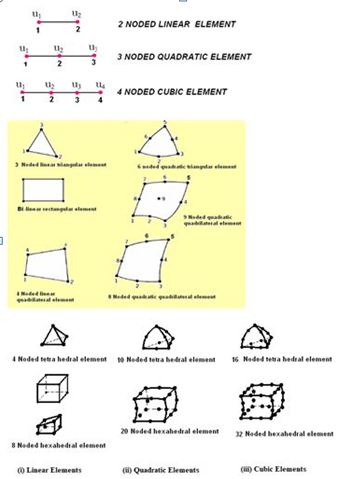
In the Finite Element Method we use several types of elements. These elements can be classified based upon the dimensionality ( ID, II D and III D Elements) or on the order of the element (Lower order and Higher order elements).

The lower order elements are also referred to as Linear elements as the displacement models and hence the shape functions are linear.

Among higher order elements we have quadratic and cubic elements where the variation of the field variables expressed in terms of shape functions are respectively quadratic and cubic. The figures shown below show some ID, 2D and 3D linear and quadratic elements

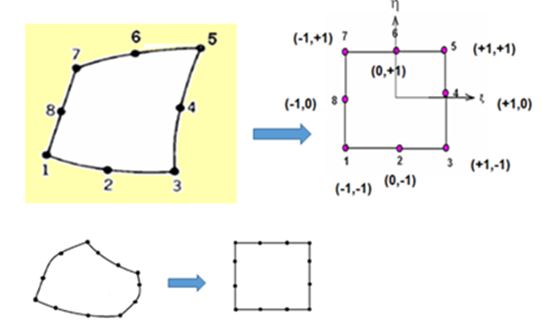
Now , it can be seen that higher order elements in 2D and 3D may have curved sides. Because of this we cannot derive the shape functions easily. Hence we map these elements into natural coordinates space where the absolute coordinates of each element does not exceed unity (one). When mapping a curved side element it becomes a square of size 2 x 2. We can then use some method of deriving shape functions keeping in mind the properties of shape functions. (Has a value one at the node it is associated with and a value zero at all other nodes).

The figures shown above shows how a curved side element in Cartesian coordinates becomes a regular square shaped element when mapped to natural coordinate space.

Now when these elements are transformed to Natural coordinate space we also derive the shape functions in terms of Natural coordinates. These shape functions are used not only for field variable approximation but also for the mapping from Cartesian space to Natural Coordinate space.

Now when deriving the Stiffness matrix elements we need to evaluate derivative of the shape functions with respect to Cartesian coordinates.

Here J is the ‘Jacobian’ of transformations from Cartesian space to natural co-ordinate space. It can be considered as the scale factor between the two co-ordinate systems. It is given by :

Knowing the shape functions of a two noded element to be

if we evaluate the Jacobian we get l/2

Do not interpret it as a value. Here l/2 is the ratio of a the length of the two noded element in Cartesian space and 2 is the length of the element in Natural coordinate space. So it signifies the scale factor while transforming.

Now Jacobian in two dimensions is a matrix which is a measure of how much of distortion the element undergoes while mapping from Cartesian coordinates to Natural coordinates. The determinant of the Jacobian should not be negative. It becomes so when evaluated at some points when the geometry has indents ie when the element does not satisfy some geometric constraints. Quadrilateral elements should be convex.

In the two four noded elements shown below the element (a) is permissible however element (b) is not.

When we evaluate the Jacobian matrix for the element (a) it signifies how much the element has to be distorted in order to take the shape of a regular square of dimensions 2 x 2.

The significance of Jacobian can be understood from the values of the same for the two elements shown above. In the second element, the length of the element in the x direction is 2 units and along the y direction 1 unit. So no distortion in x direction but in the y direction ratio of lengths is 0.5 when mapped to an element of size 2 x 2. And as its a regular shape off diagonal values are 0 and J11 is 1 and J22 is 0.5. The same is not so for the element 1.

Hope this gives you some idea as to the Jacobian used in FEA.